快排与双轴快排

传统快排

该方法的基本思想是：

1. 先从数列中取出一个数作为基准数
2. 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边
3. 再对左右区间重复第二步，直到各区间只有一个数

快速排序还有很多改进版本，如随机选择基准数，区间内数据较少时直接用另的方法排序以减小递归深度

示例代码如下, 没有进行任何优化操作, 便于更直观的理解

public class ArraysTest {

    public static void main(String[] args) {
        int[] arr = new int[]{5, 6, 1, 3, 9, 8, 0};
        System.out.println(Arrays.toString(sort(arr)));
    }


    public static void sort(int[] arr, int i, int j) {
        if (i < j) {
            int start = i;
            int end = j;
            int pivot = arr[i];

            while (true) {
                while (true) {
                    if (i == j) {
                        break;
                    }
                    if (arr[j] <= pivot) {
                        arr[i] = arr[j];
                        break;
                    }
                    j--;
                }

                while (true) {
                    if (i == j) {
                        break;
                    }
                    if (arr[i] > pivot) {
                        arr[j] = arr[i];
                        break;
                    }
                    i++;
                }

                if (i == j) {
                    break;
                }
            }
            arr[i] = pivot;
            
            sort(arr, start, i - 1);
            sort(arr, i + 1, end);
        }
    }
}

双轴快速排序(Dual Pivot Quicksort)

经典快排进行了更多的元素扫描动作，因此也就比较慢。

Dual-Pivot快排比经典快排节省了12%的元素扫描，从实验来看节省了10%的时间

双轴快排使用了两个pivot, 即双轴, 双轴隔断(partition)后

区间如下

[n < p1, p1 <= n <= p2, n > p2 ]

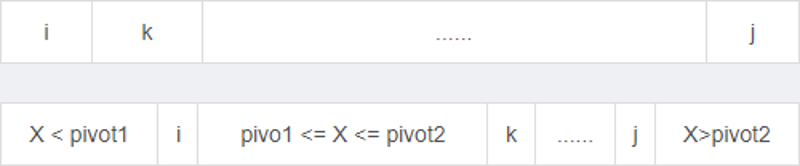
left为0, right为最后一位下标

Part I [left, i - 1]为 < P1 部分

Part II [i, k - 1]为 >= P1 且 <= P2 部分

Part III [j + 1, right - 1]为 > P2 部分

Part IV [k, j] 为还没有确定的部分
排序中, 通过k的遍历, 逐一确定每一个元素所在区间, 并进行对应交换

如下数组, 初始化i=0, j=length-1, k=i+1, 若p1>p2, 需要交换两个轴的位置, 即swap(arr[i], arr[j]), p1=arr[i], p2=arr[j]

因为当第一次寻找到第一区间的数时, k是与++i进行交换的, 即轴1的位置是暂时先固定, 保证i左边的数符合第一区间的条件, 最后将arr[0]这个轴放到第二区间的第一位上以符合轴左右的数的顺序.

同理, 当第一次寻找到第三区间的数时, k是与--j进行交换的. 轴2的位置固定, 保证j右边这个范围都是第三区间的数, 最后将arr[length-1]这个轴放到第二区间的最后一位上以符合轴左右的数的顺序.

第一次排序结果

4, 3, 5, 6, 7, 8 | p1 = 5, p2 = 7

完成后, 可以发现p1左边都是小于等于p1的, p1/p2中间的都是大于p1, 小于等于p2的, p2右边都是大于p2的

最后将三个区间再进行递归排序即可

代码如下

public static void main(String[] args) {
    int[] arr = {5, 5, 8, 6, 4, 3, 7};
//        int[] arr = {4, 981, 10, -17, 0, -20, 29, 50, 8, 43, -5};
//        int[] arr = {3, 5, 67, 54, 2, 56, 0, 7, 134, 23};
//        int[] arr = {3, 5, 1, 6, 4, 7, 2, 8};
    dualPivotQuickSort(arr, 0, arr.length - 1);
    System.out.println(Arrays.toString(arr));
}

public static void dualPivotQuickSort(int[] arr, int i, int j) {
    if (i < j) {
        if (arr[i] > arr[j]) {
            swap(arr, i, j);
        }
        int k = i + 1;
        int p1 = arr[i];
        int p2 = arr[j];
        int start = i;
        int end = j;

        while (k < j) {
            if (arr[k] < p1) {
                // 第一区间
                // 先自增再交换
                // 如果不自增直接交换, 可能会将轴放到错误的位置上
                i++;
                swap(arr, i, k);
                // 指针k移动到下一位
                k++;
            } else if (arr[k] >= p1 && arr[k] <= p2) {
                k++;
            } else {
                while (true) {
                    // 如果不自增直接交换, 可能会将轴放到错误的位置上或跳过元素
                    j--;
                    if (arr[j] <= p2 || k >= j) {
                        break;
                    }
                }
                // 指针重合 退出循环
                if (k >= j) {
                    break;
                }
                swap(arr, k, j);
            }
        }
        // 将两个轴放在隔断(partition)处
        swap(arr, start, i);
        swap(arr, end, j);
        // 将两轴隔断形成的三区域再排序 两个轴不参与再排序, 因为本身就是有序的
        dualPivotQuickSort(arr, start, i - 1);
        dualPivotQuickSort(arr, i + 1, j - 1);
        dualPivotQuickSort(arr, j + 1, end);
    }
}

private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}